Sierpinski & Co

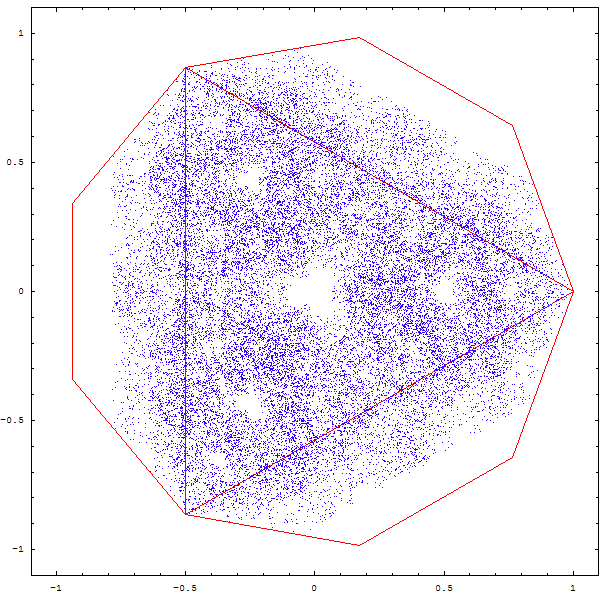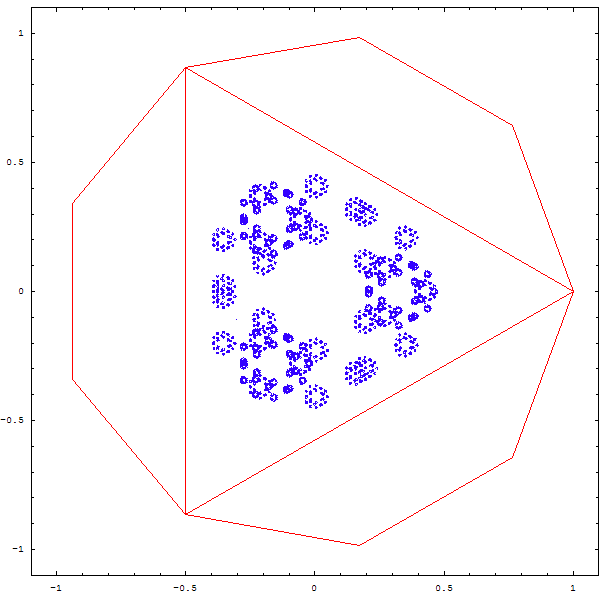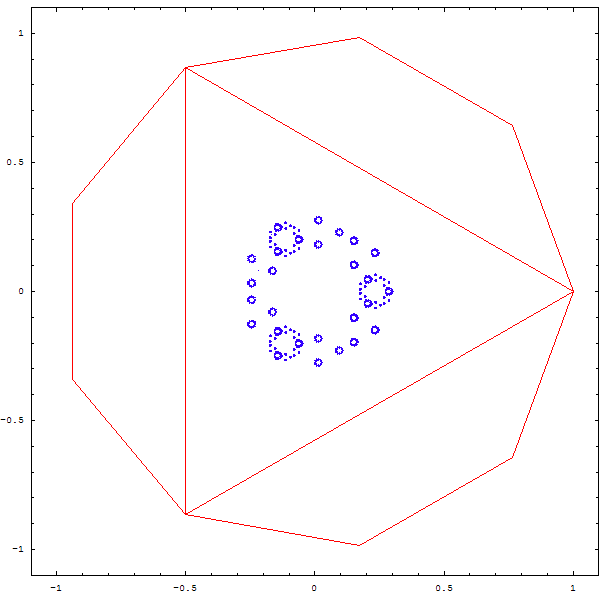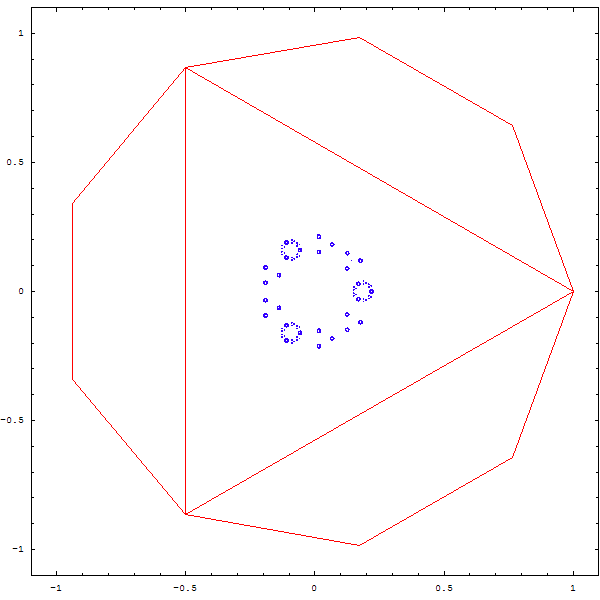
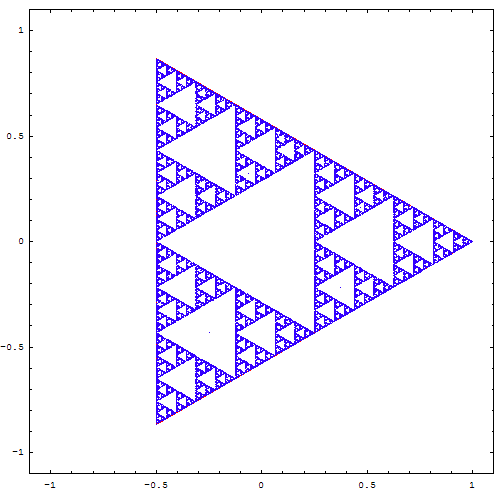
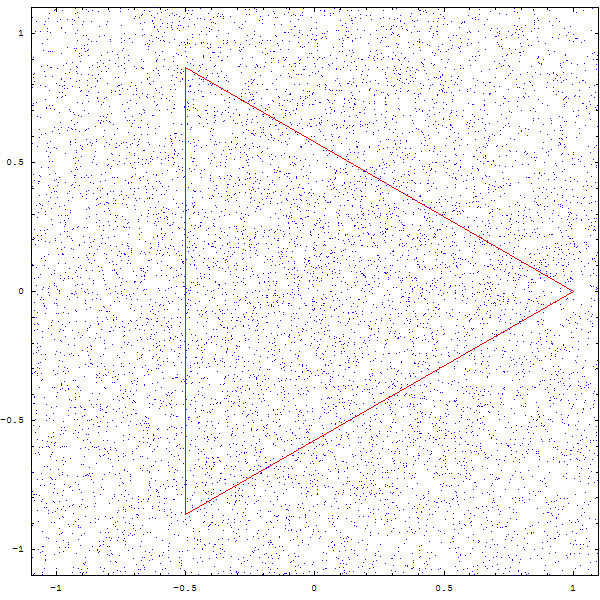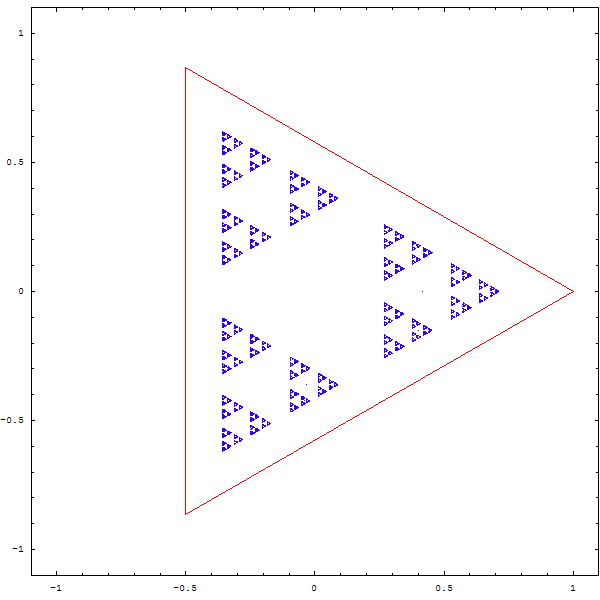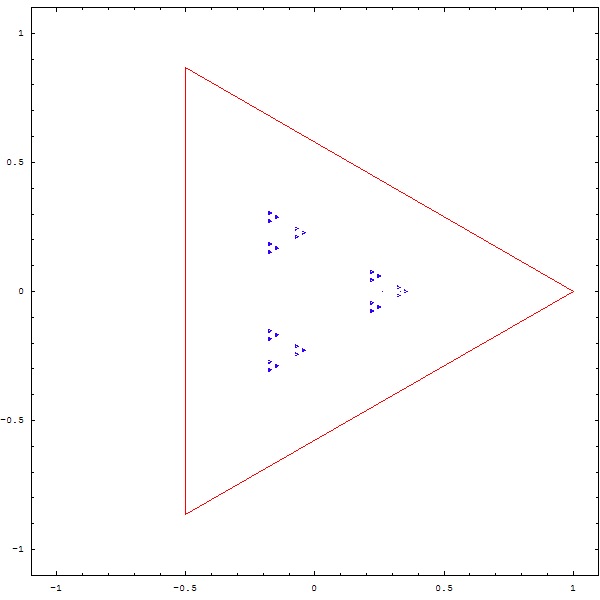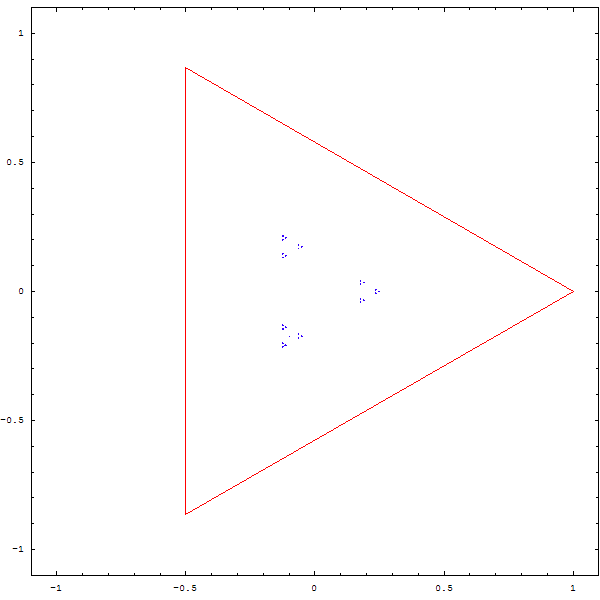
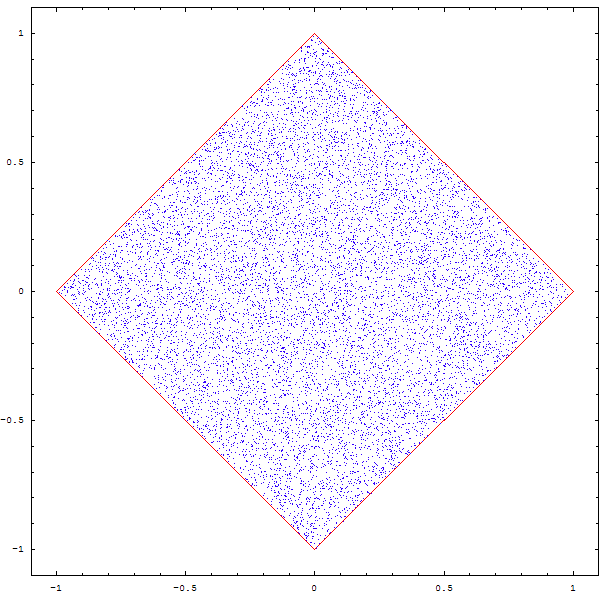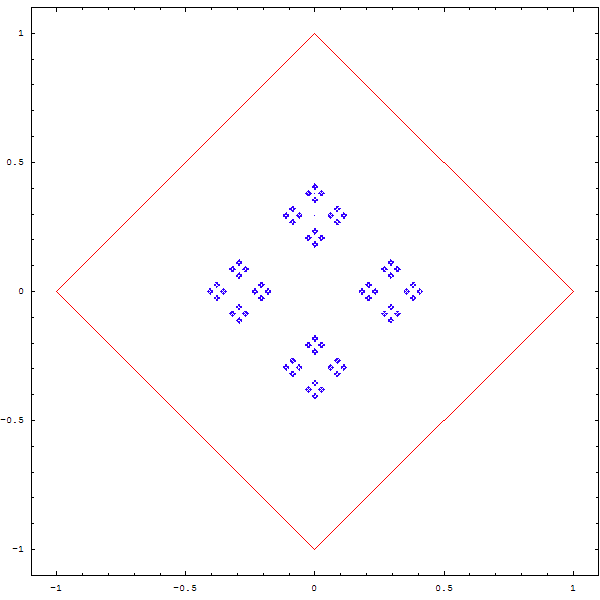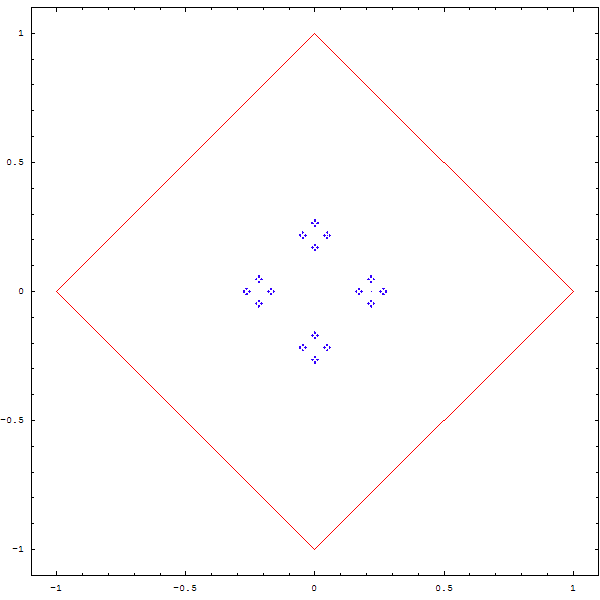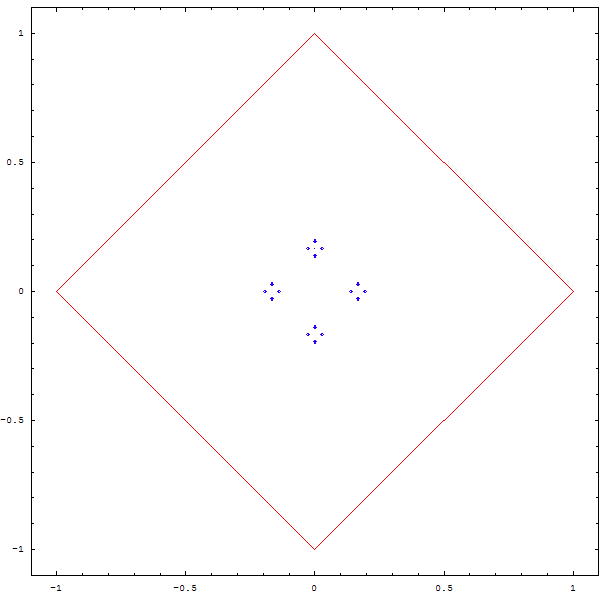
Tout d'abord, connaissez-vous le triangle de Sierpinski ?

Pour obtenir cette figure, on part d'un triangle équilatéral (3 côtés de même longueur). On choisit un point P au hasard à l'intérieur de ce triangle et on choisit également au hasard un des 3 sommets : appelons-le S1. On calcule alors le point P1 qui se trouve exactement au milieu de P et de S1. Depuis P1 , on recommence : on choisit un sommet au hasard, puis on calcule le point au milieu de P1 et de ce nouveau sommet. On appelle ce point médian P2, et on recommmence un grand nombre de fois.

La figure qu'on obtient finalement est toujous la même :

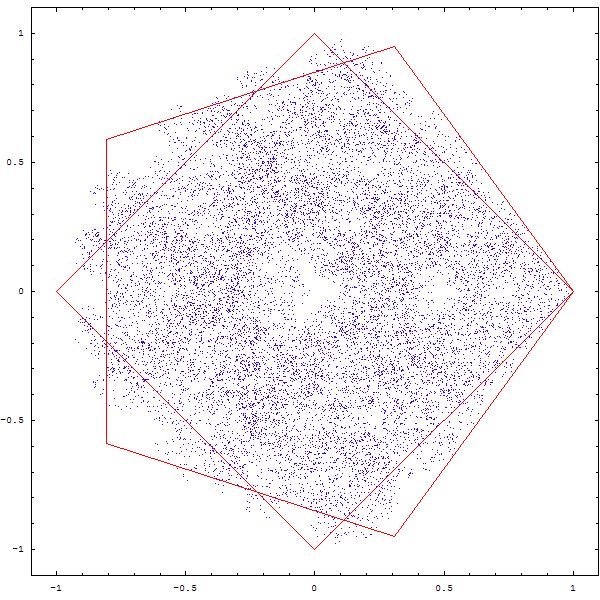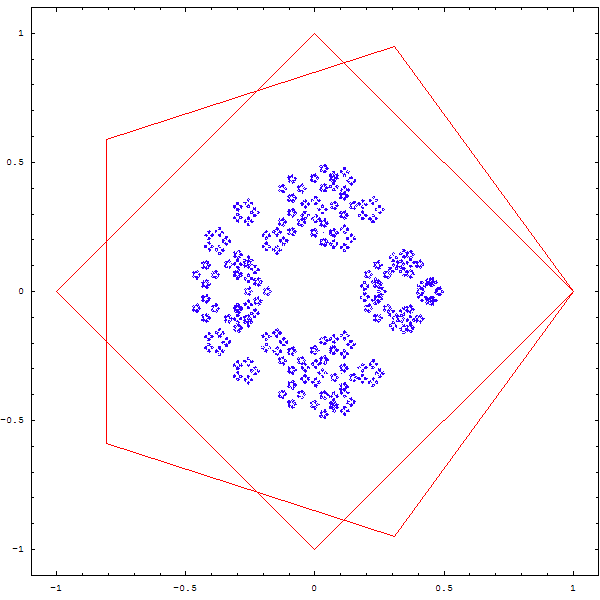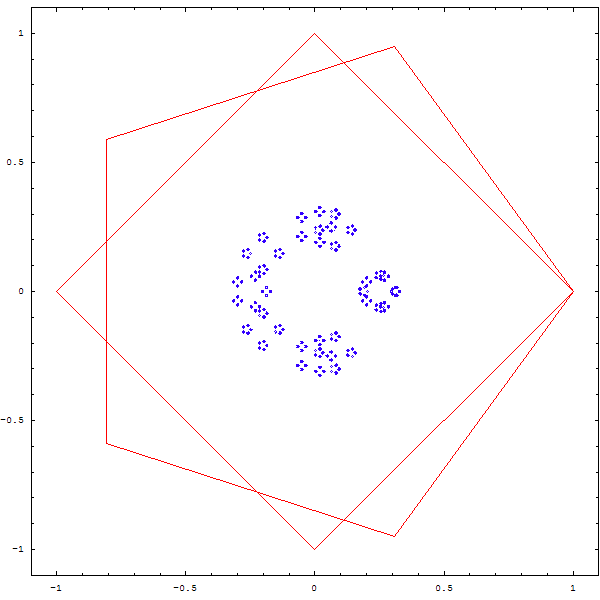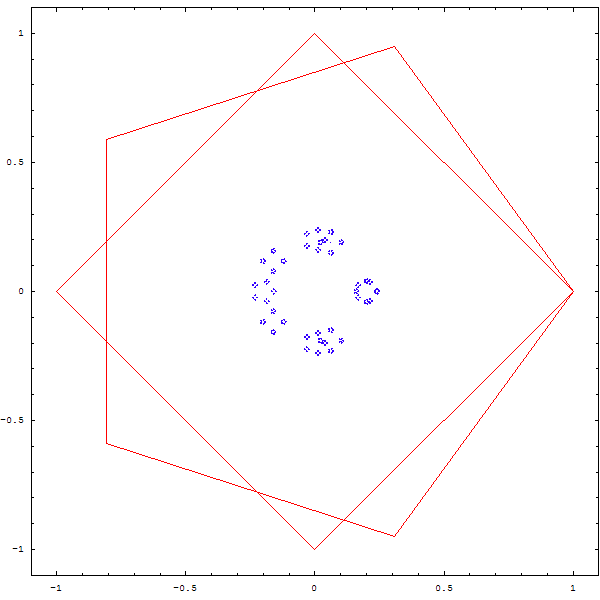
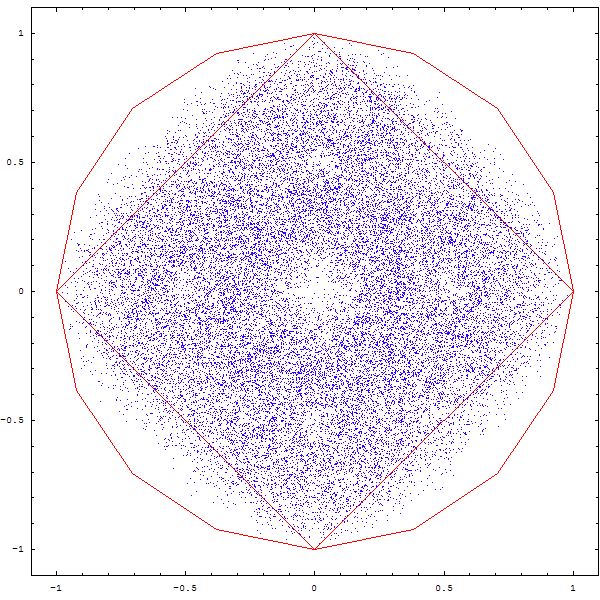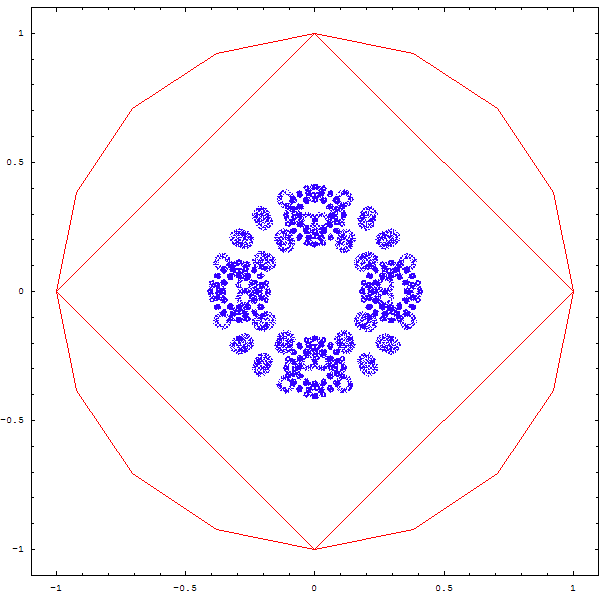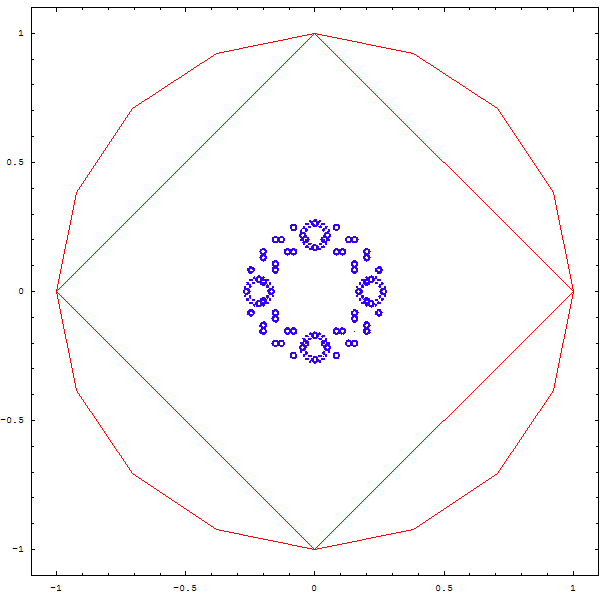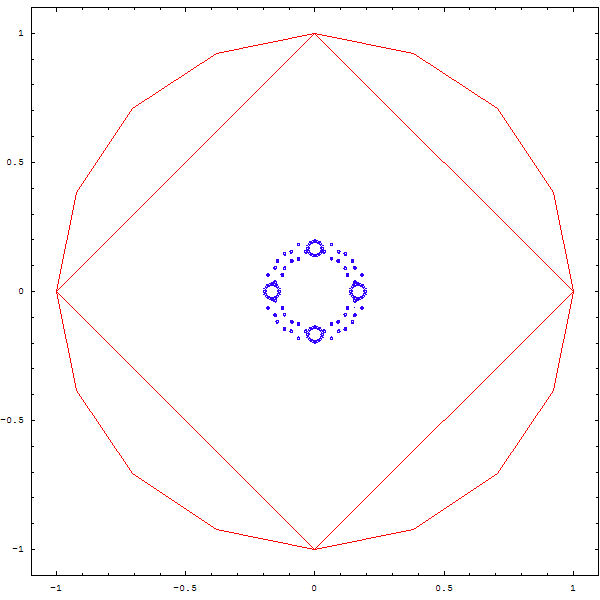
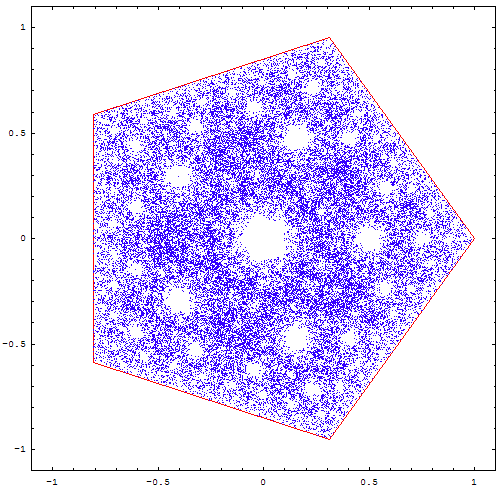
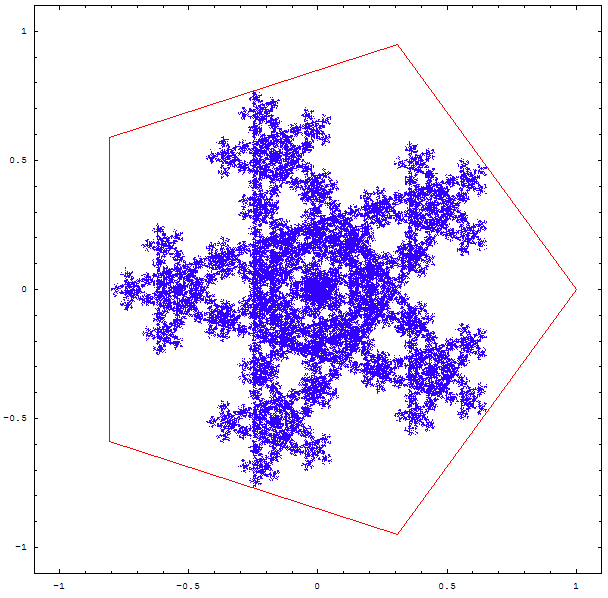
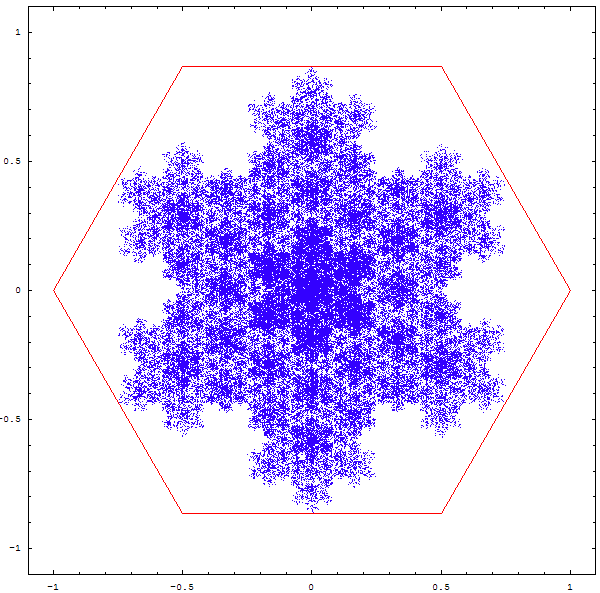
On peut se demander ce qu'il adviendrait si on était parti d'un autre polygone...

On obtient parfois des figures intéressantes, mais pas toujours très nettes, à ce stade :

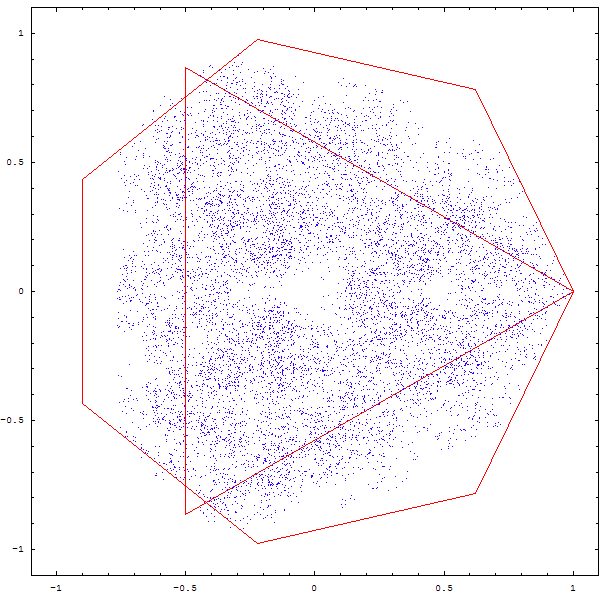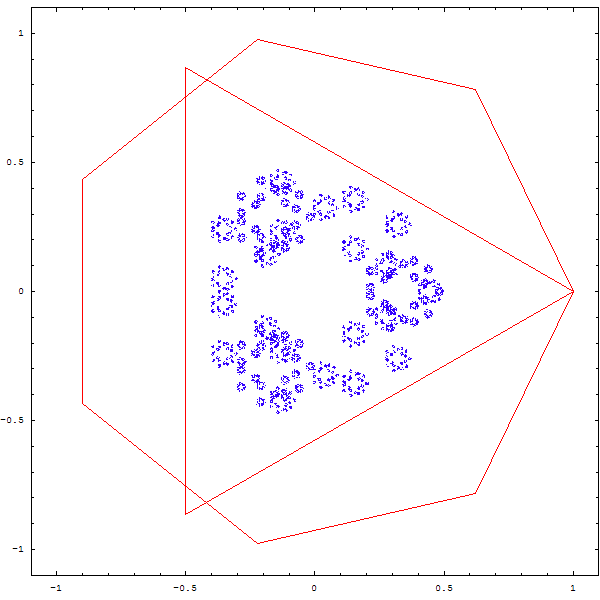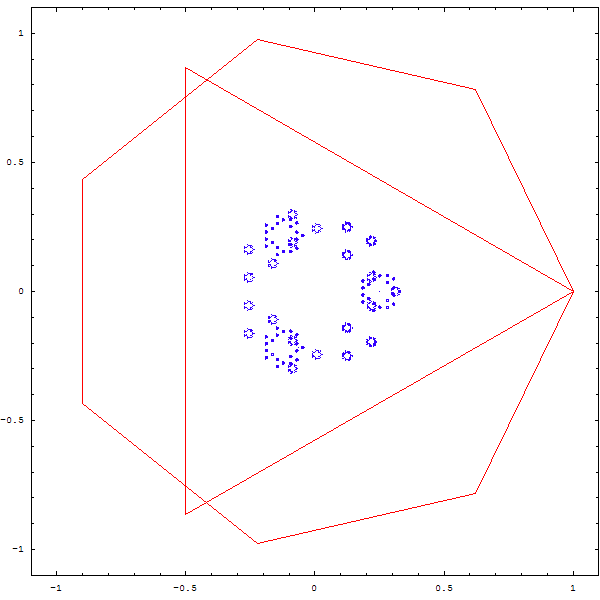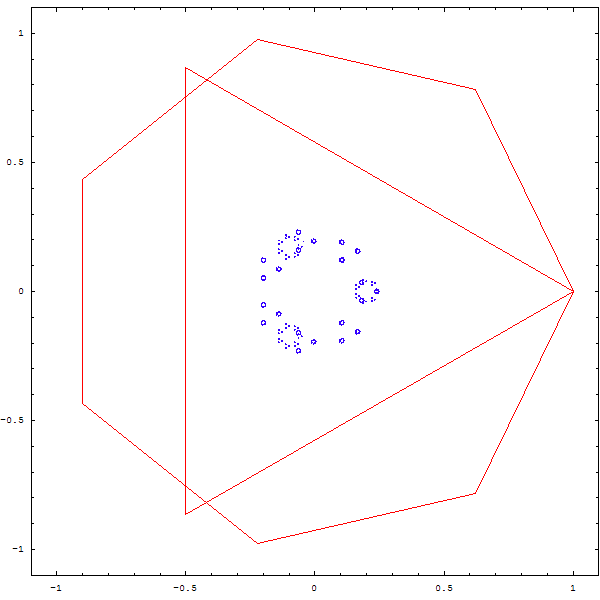
Et si l'on changeait la règle du jeu ?

On tire au sort 2 sommets, et le point qu'on dessinera est le barycentre du petit triangle formé par le point précédent et les deux sommets. Puis on recommence, bien sûr !

On obtient les magnifiques fractales ci-deesous :

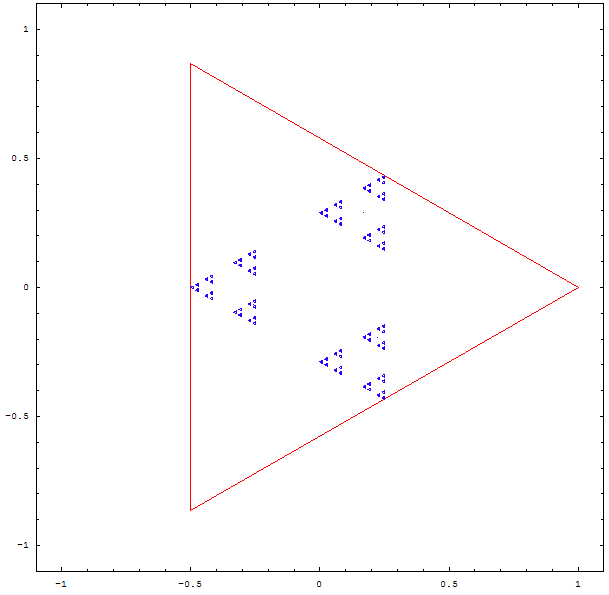
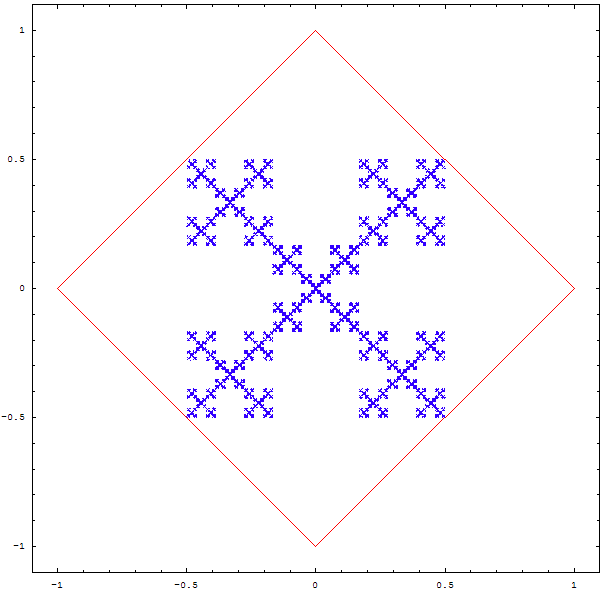
Une autre question que l'on peut se poser est la suivante : que devient une figure si on divise la distance entre le point et le sommet aléatoire non pas par 2, mais par 3, par 4 , par 5 ?

Et... du moment qu'on y est, autant en faire une animation, non ?

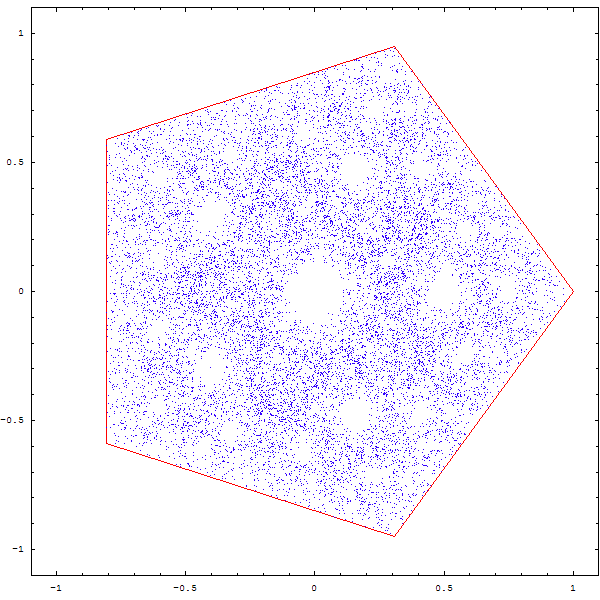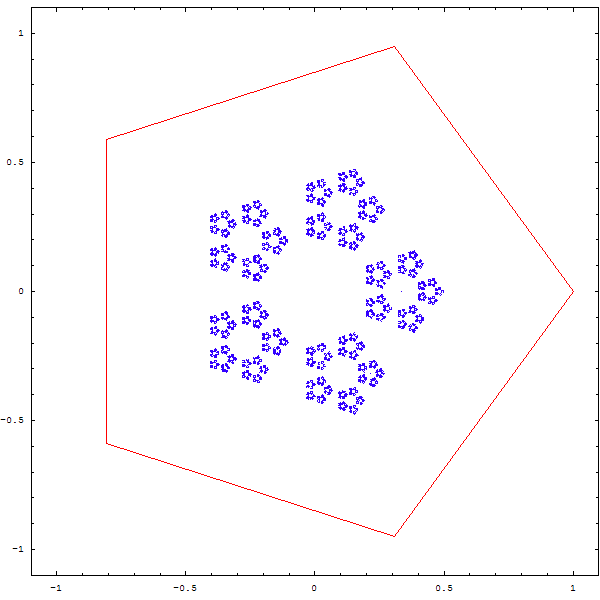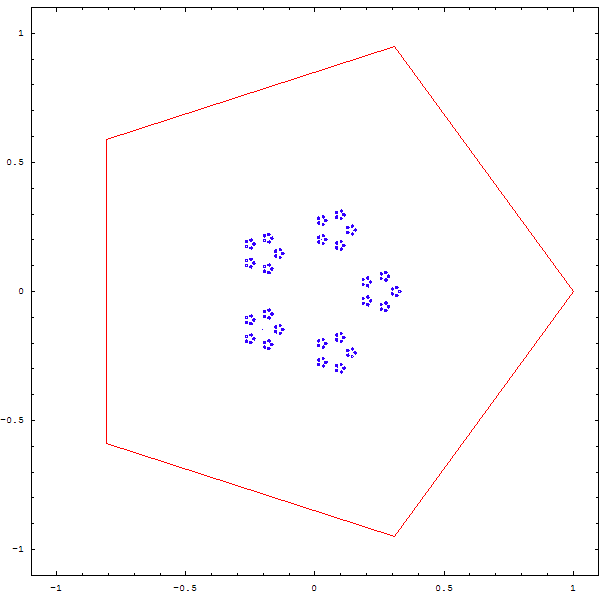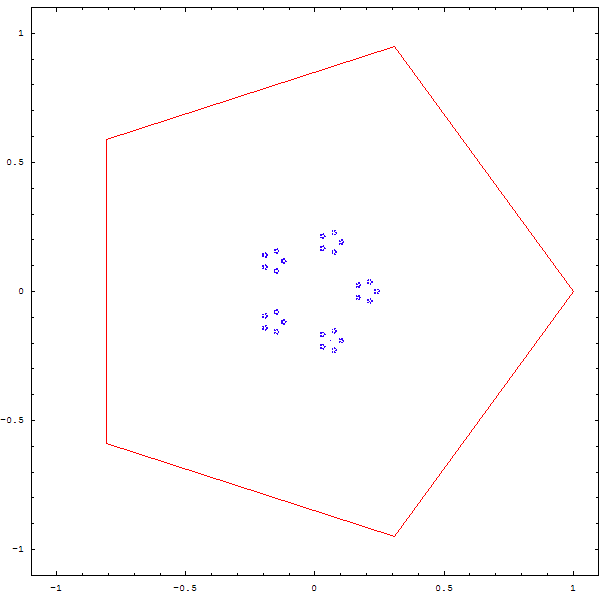
Curieux, non ? Et que se passe-t-il quand on superpose deux polygones A et B, et que depuis un point aléatoire, on choisit une fois sur deux un sommet aléatoire de A, et une fois sur deux un sommet aléatoire de B ? Et... qu'en plus on se demande ce qu'il advient si on ne divise pas la distance par 2, mais par 2.1 ou 2.3, ou...

Voici quelques exemples :